Изучение процессов электростимуляции требует создания адекватных моделей, описывающих закономерности передачи стимулирующего воздействия от выходных каскадов аппаратуры к возбудимым нервным структурам, генерации и проведения возбуждения в нервных тканях. Характерным объектом приложения воздействия при электронейростимуляции является нервное волокно, в котором под действием стимулов образуется нервные импульсы - потенциалы действия, распространяющиеся от тела клетки и ее пресинаптическим окончаниям.

В соответствии с методикой электронейростимуляции раздражающие электроды, соединенные с источником стимулирующего тока, располагаются в проекции нервного проводника, подлежащего возбуждению. В результате в межэлектродном промежутке образуется ионный ток, воздающий в тканях пространственное распределения потенциала. Возбуждение нерва происходит в случае смещения мембранного потенциала участка нервного волокна (его деполяризации до некоторого порогового значения за счет действия электрического поля стимула. После достижения порога возбуждения, определяемого свойствами мембраны нервного волокна, включаются регенеративные электрохимические процессы генерации потенциала действия, распространяющегося далее по нерву. Для создания определенной ритмичности возбуждения, имитирующей биоэнергетическую активность нерва, стимулирующее воздействие может быть сформировано в виде импульсной последовательности требуемой частоты повторения.

Закономерность возбуждения нервных проводников исследуют с помощью биофизических моделей мембранных процессов, приводящих к генерации потенциала действия. Осевая симметрия нервного волокна, близость его формы к цилиндру, однородность свойств аксоплазмы, мембраны и внеклеточной жидкости позволяют для теоретического рассмотрения процессов использовать "кабельную" модель, описываемую сосредоточенными параметрами / 1, 2 /. При условии постоянства внутриклеточного потенциала в направлении, перпендикулярном к поверхности волокна, градиент потенциала остается только в осевом направлении.

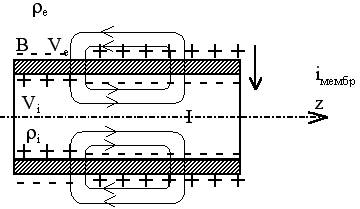
Для "кабельной" модели нервного проводника (рис.1) уравнения электрического поля стационарных токов имеют вид:

Рисунок 1 - Кабельная модель нервного проводника

Уравнения трансмембранного потенциала, полученное из выражения (1), имеет вид

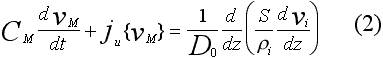
где 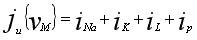- ионная компонента плотности тока, составляющие которой определены в соответствии с феноменологическими моделями мембранных процессов. Наибольшей полнотой писания этих процессов обладают модели Ходжкина-Хаксли для аксона кальмара, Нобла для волокон Пуркинье, Франкенхаузера для миелизированного нервного волокна.

Для исследования процесса электростимуляции миелинизированного нервного проводника используем решение "кабельного уравнения (2), предполагая, что миелиновая оболочка является идеальным изолятором, т.е. ее проводимостью можно пренебречь по сравнению с проводимостью мембраны, аксоплазмы и внеклеточной жидкости. Предположим также, что внеклеточное поле фиксировано и процессы в нерве не влияют на его характер. Данное упрощение не искажает эффектов действия поля при внеклеточном приложении стимуляторов, что имеет место в подавляющем большинстве методик электростимуляции, используемых в медицине. Для описания мембранных процессов воспользуемся уравнением Ходжкина-Хаксли в модификации Франкенхаузера для миелинизированного нерва.

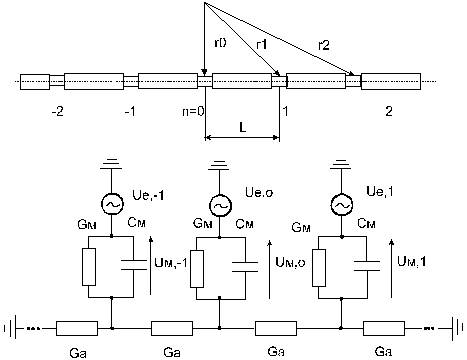
Рисунок 2 - Модель миелинизированного нервного волокна при учете распределения поля вдоль оси волокна

При нахождении нервного волокна в электрическом поле стимулирующего тока трансмембранные потенциалы перехватов смещаются в соответствии с изменением величин внеклеточных потенциалов. Для случая точечного электрода, расположенного на расстоянии r0 по нормали к "нулевому" перехвату (k=0, рис.2), потенциалы перехватов:

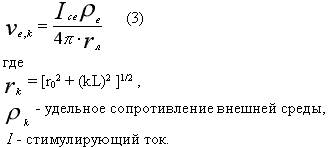
Тогда в пределах принятых допущений установления напряжений на мембранах перехватов, симметрично расположенных относительно электрода, описывается системой дифференциальных уравнений

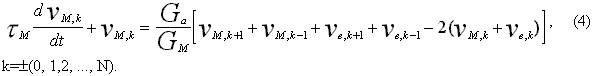
Учет в системе дифференциальных уравнений нелинейных свойств мембраны в виде уравнения Ходжкина-Хаксли в модификации Франкенхаузера, наиболее полно моделирующего процесс возбуждение миелинизированного нерва, позволяет с наилучшим приближением описать процессы, происходящие при электронейростимуляции. Поскольку только один перехват можно считать активным, то только в одном уравнении системы для k=0 трансмембранный ток записывается в виде:

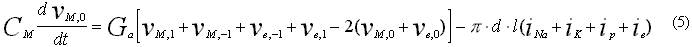
Компоненты ионных токов определены Франкенхаузером и Хаксли как

Величины 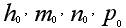 характеризующие активность ионных каналов, находятся из уравнений, описывающих соответствующие экспериментальные зависимости, наблюдаемые в процессе возбуждения волокна:

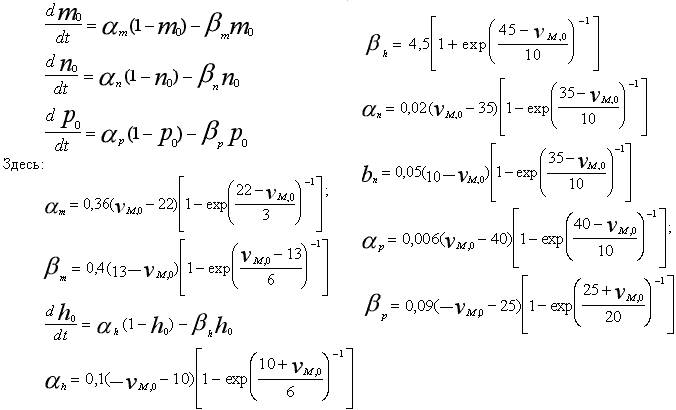
Для решения уравнения необходимо задавать начальные условия:

.

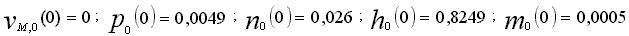Для изучения процессов электронейростимуляции методом компьютерного моделирования разработан пакет программ для ПЭВМ IBM PC "Axon", позволяющий вести исследование модели возбуждения нервного волокна при использовании стимула прямоугольной формы конечной длительности. Для модели рассчитывается величина потенциала на нулевом (ближайшем к электроду) перехвате, а также производится автоматическое определение порога возбуждения при изменении параметров стимула или параметров модели.

Пакет "Axon" включает программу, реализующую решение системы уравнений (5). В расчет берутся пять перехватов, соседних с нулевым, т.к. большее количество рассматриваемых участков нервного волокна не улучшает точность расчета, но существенно усложняет его. Решение системы дифференциальных уравнений проводилось численным методом Рунге-Кутта 4-го порядка. Для автоматического определения порогового значения амплитуды стимулирующего тока использовался метод последовательных приближений.

Алгоритм работы программы моделирования включает 3 блока :

Блок 1 - Ознакомление с моделью миелинизированного нервного волокна

Блок 2 - Выбор направления исследования модели

2.1.Определение порога возбуждения по графикам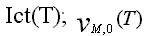 

2.2 Зависимость сила-длительность импульса

2.3 3ависимость порога возбуждения от диаметра волокна

2.4 Зависимость порога возбуждения от расстояния до электрода

2.5 Зависимость порога возбуждения от проводимости среды

2.6 Зависимость порога возбуждения от постоянной времени среды

Блок 3 Вывод результатов расчета в виде графиков.

В блоке 1 на экране компьютера отображается схема моделирования миелинизированного нервного волокна при учете распределения электрического поля вдоль оси волокна и вводятся параметры модели.

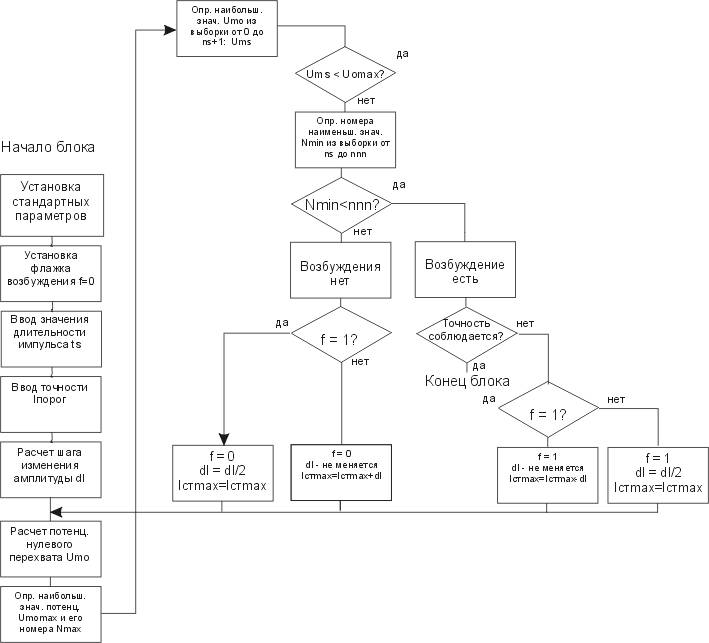
Рисунок 3 - Алгоритм расчета кривой "сила-длительность"

В блоке 2 пользователь выбирает одно из шести направлений исследования.

В случае выбора п.2.1 меню определение порога возбуждения нервного волокна происходит визуально по графику временной зависимости потенциала на нулевом перехвате. При вводе различных значений амплитуды стимулирующего тока, рассчитываются два графика - временные зависимости стимулирующего тока и напряжения на нулевом перехвате. Порог возбуждения определяется подбором такого значения амплитуды стимула, при котором наступает возбуждение.

В случае выбора одного из п.2.2-2.6 определение момента возбуждения производится программой автоматически, путем изменения амплитуды стимулирующего воздействия, расчета потенциала и проверки наличия возбуждения с помощью анализа множества значений потенциала. Алгоритм программы (рис.3) дан на примере п.2.2 - исследования зависимости "сила-длительность".

Формирование напряжения на мембране для допороговых и сверхпороговых стимулов, полученное с помощью рассматриваемой модели миелинизированного нервного проводника, показано на рисунке 4. Проводимость мембраны по мере приближения к порогу возбуждения изменяется сначала медленно, затем все быстрее по мере того, как возрастает проницаемость мембраны для ионных компонентов тока. При уменьшении амплитуды стимула возбуждение наступает при больших длительностях воздействия. Регенеративный характер процессов, возникающих при возбуждении волокна, хорошо виден при стимуляции импульсами постоянной длительности (рис. 4).

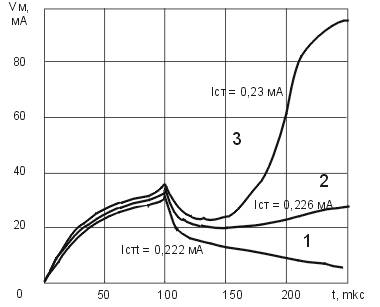
Рисунок 4 - Формирование мембранного потенциала при стимулах постоянной длительности и различной амплитуды

При сверхпороговых амплитудах потенциал действия возникает после отключения стимула (кривая Iст=0,23 мА), являющегося толчком к возникновению генераторных процессов формирования напряжения на мембране. Возбуждение нервных структур при электронейростимуляции описывается зависимостями "сила-длительность", представляющими собой соотношения между амплитудой и длительностью порогового стимула при различных условиях стимуляции и параметрах модели.

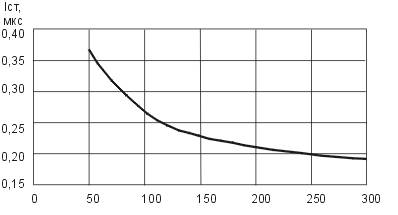
Рисунок 5 - Кривая сила-длительность

Наибольший практический интерес представляет использование данной модели для определения пороговой интенсивности стимула при изменении различных параметров как стимула, так и самого нервного волокна. Решение уравнений модели при различных начальных условиях позволяет определить влияние геометрии системы "электрод - возбуждаемый нервный проводник" на изменение проводимости межклеточной среды, а также определить закономерности возбуждения для волокон различного размера.

Модель возбуждения миелинизированного нервного проводника соединяет в себе феноменологические представления о генерации потенциала действия, наиболее близко описывающие физиологическую картину возбуждения и электрофизические закономерности образования деполяризующего потенциала при внеклеточном расположении стимулирующего электрода. Поэтому данная модель позволяет исследовать характеристики возбудимости при изменении как параметров стимулов, среды, окружающей нерв, нервного волокна, так и геометрии системы "электрод - нервный проводник". Это позволяет использовать данную модель для изучения закономерностей электронейростимуляции.

Список использованных источников:

1. Титомир Л.И. Электрический генератор сердца. М.: Наука, 1980.-371с.
2. Hodjkin A., Huxley A. A quantitative description of membrane current and its application to conduction and excitation in nerve//J.Physiol. (London).-1952.-N4.-P500-544.
3. Noble D. A modification of the Hodjkin- Huxley equations applicable to Purkinge fibre action and pace-maker potentials// J.Physiol..-1962.-N2.-P.302-315.
4. Frankenhaeuser B., Huxley A. The action potential in the myelinated nerve fibre of Xenopus Laevis as computed on the basis of voltage clamp data// J.Physiol..-1964.-N2.-P.302-315.
5. Mc Neal D. Analysis of a model for excitation of myelinated nerve // IEEE Trans. On Biomed. Eng..-1983.-v.30.-N4.-P.329-337.